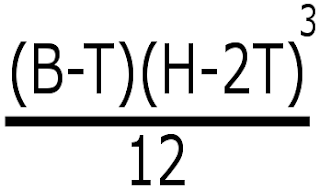Beam Calculator

The project for week 5 was to make a calculator that would calculate the deflection of a beam. In this case the beam would be made of wood and would be one of three designs. The options were: an I beam, H beam, or a box beam.

Firstly, their are some terms that need to established. The basic terms to know for now are: flange, web, width, height, and thickness of material. Here is a simple diagram that I made using Inkscape. Inkscape was used to make all of the diagrams and formulas. This diagram points out all of the aforementioned terms:

The flanges are the top and bottom, while the web is the center support. The width and height are self explanatory, but the thickness of material is important. You need the thickness in order to use these formulas and calculations.

Now that those are defined, here is how I made the calculator:

I knew that in order to make a working calculator I would need formulas. A calculator needs formulas so that the values can be set to a variable. Then the variables are plugged into the formula and it spits out the answer. So the first thing I did was to get the formulas that Dr. Harris gave us. These were the Moment of Inertia and the Deflection formulas.

The formula for Moment of Inertia is this:

B = base or width of beam
H^3 = height of beam cubed
Multiple both together and then divide by twelve

This formula works for a solid beam, but what about and I beam? An I beam has two empty spaces on either side of the web. These spaces need to be removed from the formula as there is no support there. This can be done by finding that area and subtracting it from the whole area. The whole area is dubbed as positive space, or I-pos. The empty area is dubbed as negative space or I-neg. Here is a diagram to demonstrate positive versus negative space:

How we find I-neg is to remove the top and bottom, known as flanges, from the area. This can be done if we know the thickness of material. We take the thickness of material and multiply it by two and then subtract it from the height. We also need to get rid of the web. This can also be done if we know the thickness of material. Simply subtract the thickness from the base or width.

I then came up with a modified formula to find the negative area:

B = base
H = height
T = thickness

This formula allows you to take the base, height, and thickness of material and plug them in directly. (Base minus thickness) times (height minus 2 thickness) cubed and then divided by twelve. This gives you the actual area known as I-total. This is the Moment of Inertia. The result,  I-total, is used in the deflection formula. Here is the deflection formula:

P = concentrated load in Lbs
L = length, typically the span
E = Modulus of Elasticity
I = Inertia

(Load times span) cubed divided by (48 times Elasticity times Inertia)

Span is another term that needs clarification. The span of the beam is the distance between the two points of contact. Another way to think of span is the gap that the beam spans. The length is the overall length. This is used for calculating the weight. Here is a diagram showing length versus span:

I was able to use the deflection formula with any modification. However I did substitute the Modulus of Elasticity for the elasticity of basswood. The calculator is a one trick pony. It will only calculate the Moment of Inertia and Deflection for a basswood I-beam. The elasticity of basswood is 1,460,00 Lbs/in^2 or PSI. This means that  basswood will spring back until 1,460,00 pounds of force are applied. Basswood is fairly springy.

Once the formulas were squared away, the next step was programming. I decided not to start from scratch and use some existing code. I used some of my existing unit converter code plus some code that another person wrote. Dr. Harris recommended the class to look at the old classes and I came upon some usable code. The code was basic and in all honesty, pretty bad. Here is the student's page that wrote the code. The calculator had some odd formulas in it, the inputs were basic, and only one output.

I took my code, the aforementioned code, and a little bit of another code and made them into a working calculator. Here is her page for this calculator. I took the main layout of the rough code and stripped down to the bare codding. The only things I kept were the text boxes and the output coding. The main piece of coding that came from the second code was the text withing the text box. This is fairly simple, you create the basic text box code and then write in 'placeholder="namehere" '. Simply replace the namehere with whatever you want the text box to display.

placeholder="name"

Basic Beam Calculator

This is a calculator for a basswood I-beam.
This calculator has two fixed variables, the density and elasticity.
The maxium density of basswood is 37 Lbs per cubic Ft
The elasticity of basswood is 1,460,000 Lbf per square inch.

(in)
(in)
(in)
(in)
(in)

(Lbs)



(in^4)

(in)

(lbs) Here is my code in JSbin
Here is my code in a .txt format

The final design of the calculator is fairly straight forward. It is fixed for a basswood I-beam, as that is what I will be using. There are two fixed variables because it is made for basswood. These variables are the density and elasticity. This does make the calculator simpler for the average person as not many people would know the density or elasticity of basswood.

The major design change from the other calculators that I have seen is this: the diagrams are embedded into the HTML script. Once again, it clarifies which dimension is which and ensures that the correct values will be used. The code changes are fairly major, I as stated most of the existing code was stripped, removed, or trashed completely. The two biggest changes were the number of outputs and the formulas.

Overall, this project was time consuming and aggravating. The hardest part was getting the code to display the proper outputs. The overall time spent on this project was 10 - 12 hours. This calculator made me realize that there are a million different was to program the same thing. However, some ways are better than others. I did learn a lot, such as placeholder display, and it reinforced the idea that you do not need to start from scratch. Here is my code in a text highlighter:

<!DOCTYPE html>
<html>
<head>

  <script>
  function calculatefunction(){
    //Width = base. Set width to variable B:
  var B = document.getElementById("width").value; 
    //Set height to variable H:
  var H = document.getElementById("height").value;
    //Set thickness to variable T:
  var T = document.getElementById("thick").value;
    //Length = span. Set length to variable L:
  var L = document.getElementById("length").value;
    //Concentrared load = P. Set load to variable P:
  var CL = document.getElementById("load").value;
    //Set span to variable S
  var S = document.getElementById("span").value;
    
    //Find positive space (b*h^3)/12
  var Ipos = ((B) * (H*H*H)) / 12;
    //Find negative space, two negative spaces. ((Width - 1 thickness) * (h-2t)^3)/12
  var Ineg = ((B - T) * ((H - (2 * T)) * (H - (2 * T)) * (H - (2 * T)))) / 12;
    //Find Itotal:
  var Itotal = Ipos - Ineg;
    //Formula for Delta: ((P)(S^3))/(48(E)(I))
    //The average Modulus of Elasticity for basswood is 1,460,000 Lbf/in^2. I am simply substituting for E.
  var Delta = (CL * (S*S*S))/(48 * 1460000 * Itotal);
    //Output Delta as Deflection:
  var Deflection = document.getElementById("deflectionid");
   Deflection.value = Delta;
    //Out put Itotal as Inertia in in^4
  var inertiaAnswer = document.getElementById("inertiaAnswer");
   inertiaAnswer.value = Itotal;
    //Calculate density:
      //Density = mass/volume
      //Max density of basswood = 37 Lb/ft^3
      //37 Lb/ft^3 * 1ft^3/(12in)^3 = 0.02141 Lb/in^3
      //Density * volume = mass
  var volume = (Itotal * L);
  var mass = volume * .02141;
  var MoB = document.getElementById("MoB");
   MoB.value = mass;
  
  }
  </script>
</head>
<body>
  <h3> Basic Beam Calculator</h3>
  </br>
  <img src="https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhNU6wIzM2k8dTR-RQ99zGGznWntXppnraaCNTd4oq1bcXwOZcXHwKB48suqpFaVMyttrPXFYmTj7dKALVWUyQMyNm72sHca72rXN4XpkKTq1JzmKcVN-hAzencXhiKi-arBN-uqRF0FwY/s1600/I+beam+drawing.png" alt="Width, height, thickness" style="float:right;width:300px;height:200px;">
 This is a calculator for a basswood I-beam.
  </br>
This calculator has two fixed variables, the density and elasticity.
  </br>
The maxium density of basswood is 37 Lbs per cubic Ft
  </br>
The elasticity of basswood is 1,460,000 Lbf per square inch.
  </br>
  </br>
  <input type="number" placeholder="Width" name="width" id="width" /> (in)
  </br>

  <input type="number" placeholder="Height" name="height" id="height" /> (in)
  </br>
  <input type="number" placeholder="Length" name="length" id="length" /> (in)
  </br>
  <input type="number" placeholder="Span of Beam" name="span" id="span" /> (in)
  </br>
  
  <input type="number" placeholder="Thickness of Wood" name="thick" id="thick" /> (in)
  </br>
  </br>
<img src="https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiQGSFaPPB5eVd1U_QszohCfR-bjKswMOvbhGvmCJSZtzRRqEe7nT6pOOs4e_8fB3jEyVaM99EymL8EXMbZCQDURkx_lI_ZDS4Wc-CVoINO3G1auBvJJeGpSJYGerK_GOCpcx_QiF97uN8/s1600/I+beam+length+vs+span.png" alt="Length vs Span" style="float:right;width:300px;height:200px;">
  <input type="number" placeholder="Concentrated Load" name="load" id="load" /> (Lbs)
  </br>
  </br>
  <input type="submit" name="calculatebutton" id="calculatebutton" onclick="calculatefunction()" value="Calculate" />
  </br>
  </br> 
   <input type="number" placeHolder="Moment of Inertia" name="inertiaAnswer" id="inertiaAnswer" /> (in^4)
  </br>
  </br>
  <input type="number" name="Deflection" placeholder="Deflection" id= "deflectionid" readonly="true" /> (in)
  </br>
  </br>
  <input type= "number" name="MoB" placeholder="Mass of Beam" id= "MoB" readonly="true" /> (lbs)

  </body>
</html>